How does an op amp work? How do I use an op amp
These are questions that I have asked at two periods in my life. The first time was in my introductory circuits class and around that time I really didn’t care (beer was a priority). The second time was when I dove headfirst back into analog electronics for my new job and had to re-teach myself a lot of things. I really appreciate the opportunity I had to re-learn everything because the second time around, I think I got it right.
OK, so let’s start simple. What is an op amp? Whoa, loaded question. For our purposes here (and just for now), let’s say it’s just a symbol.
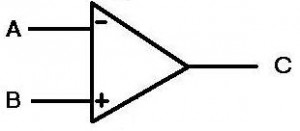
To keep things basic, the A & B points are the input, the C point is the output.This symbol is an IDEAL op-amp, meaning it is impossible to construct one and really the expectations for the op amp are unrealistic. But this is the internet and we can do what we want on the internet, so we’ll just use the IDEAL op-amp for now.
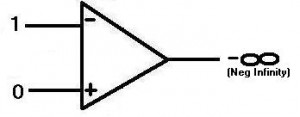
OK, so now you know what the symbol is, but what does it mean? Well, the idea is you put two electrical signals into the inputs then the output changes accordingly. It takes the difference between the inputs and amplifies it, hence operational amplifier, or op amp. You may have noticed that input A has a minus symbol and input B has a plus symbol. So let’s say that the input to the minus, or INVERTING, input is 1 (for simplicity’s sake…this site is about analog so that value could be ANYWHERE from 0 to 1 or higher! Just thought I’d mention that). The input to the plus, or NON-INVERTING, input is 0. Now the op-amp is in an unbalanced state. The device is designed so that when this happens, the output goes as negative as it can. For the ideal case, we say this is negative infinity, but that’s not really possible. More on that later.

Conversely, in figure 3, if we put a one on the non-inverting and a zero on the inverting input, the op amp output would go high, infinity for our purposes here. The important thing to know is this:
The op-amp always “wants” both inputs (inverting and non-inverting) to be the same value. If they are not, the same value, the op amp output will go positive or negative, depending on which input is higher than the other.
(Throughout this article I will continue to anthropomorphize op amps…best to get used to it now)
Alright, so how do we use this in circuits? If we wanted to find out if two signals were different, we could tie the signals to the inputs of the op amp, but then the output would go to infinity. This would not do us any good. The answer to this and many other questions in the universe is feedback. We are going to take the output and tie it back to the inverting input. Now the circuit looks like this:
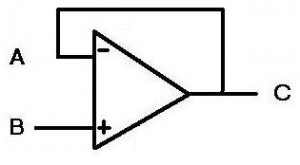
First, we assume that the circuit has all points start at zero (point A being the most important). Next, we put a value of 1 (like the picture in figure 2) at the “B” non-inverting input. “WHOA,” says the op amp, “THIS AIN’T RIGHT!” So now the op amp puts its output to as high as it can, as fast as it can. This feeds back from the output (“C”) to the inverting input (“A”). So as the output moves closer to 1, the op amp is happier and backs off the output. When the input at A is the same as at B, the op amp is happy and stays there (but maintains the output of 1). The key here is that the op amp moves as fast as possible to get both inputs to be the same.
Why would someone use a buffer? Well that brings us to the next point about op amps, specifically ideal op amps:
Ideal op amps have infinite impedance (resistance) at their inputs. This means that no current will flow into the op amp.
A common use for a buffer is to supply current to another stage of a design, where the buffer acts as a gateway. So when the buffer “sees” a voltage at the input (“B”), it will output the voltage at “C”, but will also drive that voltage with current (as much as you want for an ideal op amp). This would be useful if you have a weak signal at the input, but want to let some other part of a circuit know about it. Perhaps you have a small sensor that is outputting a small voltage, but then you want to send the voltage over a long wire. The resistance in the wire will probably consume any current the sensor is outputting, so if you put that signal through a buffer, the buffer will supply the necessary current to get the signal to its destination (the other end of the wire).
What if the signal coming from the sensor is too small though? What if we want to make it bigger? This is when we turn the op amp into an amplifier, using resistors. One of the more common ways of doing so is using the inverting input, shown below:
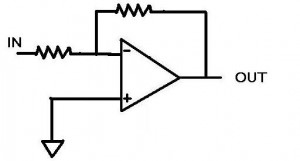
Let’s go over what we know about this circuit. We know that the op amp wants both inputs to be the same. We also know that the non-inverting input is zero (because it’s connected to ground) and so the op amp will want the inverting input to be equal to zero (sometimes known as a “virtual ground”). In fact, since the op amp has feedback through the top resistor (squiggly line if you didn’t know), then the (ideal) op amp will output just about any current and voltage in order to get the inverting input to be equal to zero.
So now our situation. A dashing young engineer hooks up a voltage source to the point “IN” set to 1 volt. This creates a voltage at the inverting input. “WHOA” says the op amp, and then it begins to output a voltage to make the inverting input point equal to zero. Since the input is 1 volt the op amp decides it better do the opposite in order to make the inverting input match the non-inverting input of zero. As fast as it can (infinitely fast for an ideal op amp), it outputs -1 volt. The inputs are both zero and everything is right in the op amp’s world. What about current though? We remember that current cannot flow into the op amp at the inverting input, so any current will be flowing through both resistors. If we have 1 volt at the input and a 1 ohm resistor at the input, then we will have 1 amp of current flowing (according to Ohm’s law V=IR). So when the op amp outputs -1 volt across the top resistor, there is a -1 amp going through it (assuming it is a 1 ohm resistor). The currents cancel each other out at the inverting input and the voltage then equals zero. The place where the currents meet is sometimes called the “summing node”. This is a useful representation when dealing with currents as opposed to voltages.
For the last part of this thought exercise, let’s look at a situation where the resistors at the input and at the top of the circuit are not the same. Similarly to above, the same dashing young engineer puts 1 volt at the “In” node. The resistor is still 1 ohm, so there is 1 A of current flowing through to the summing node. The op amp once again sees this 1 volt and once again says “WHOA, I’m unhappy about this” and starts outputting the highest voltage it can. However, in this situation, the top resistor is now 4 ohms. In order to create the -1 amp that is required to cancel the 1 amp going through the input resistor, the op amp must output -4 volts (remember V=IR). We see that for an inverting op amp configuration, the ratio of the resistance of the top resistor to the bottom resistor determines the gain, or a multiplication factor from the input to the output. Also notice that the output is negative for a positive input, confirming that this is an inverting amplifier.
That’s the basics of it. Check back here for more about op amps, because there is a lot more to be said. Future posts might include other op amp configurations, design considerations and even the dreaded “REAL WORLD”, where the ideal op amp no longer exist.
[xyz_lbx_default_code]